
Understanding stroke with Bayesian networks
Introduction
Stroke is a major source of morbidity worldwide, causing 5.78 million deaths per annum as per WHO global health estimates (1). An international effort is underway to improve outcomes in stroke by means of secondary and tertiary preventative measures. To maximise the efficacy of such interventions, we must fully understand the processes which lead to stroke-related morbidity and mortality. We propose to reframe stroke as a component of a network system, with multiple interacting causes and consequences. In real-world epidemiology, interactive systems are known to exist between social, behavioural and biological risk factors. The network paradigm accommodates such complexity well, and has demonstrated value in genetics (2), pathology (3-5) and therapeutics (6-8). We propose Bayesian network inference as a hypothesis-free method of characterising the causal processes of stroke outcomes.
Causal networks in medicine
The sequence of events which follows an episode of stroke is a variable and complex process. Factors such as aetiology, time-to-treatment, comorbidities, and therapy vary between individual patients and presentations. The occult interplay of such phenomena greatly complicates the procedure of hypothesis testing on the true underlying pathological process. In each domain of clinical research problems may arise due to multidimensional confounding. Analyses such as multivariate regression and naïve Bayes assume independent sampling of all observed variables (9,10). In the medical field, where biological, clinical and social factors have multiple consequences, such broad assumptions of variable independence are often inappropriate. Unobserved interactions in the causal chain between predictor and outcome variables may subsequently influence the observed significance of their relationship (10). Several epidemiological studies have concluded that such confounding may be minimised with appropriate network modelling techniques (11-13). Ultimately, phenomena which are observed in the clinical setting may be better considered as a functional system, where disease states, treatments and clinical events each have causes and consequences. The “network” approach to causality modelling has proved insightful in genetics (2), pathology (3-5) and therapy (6-8). Graphical modelling methods make few assumptions about the dependence structure of the observed variables, allowing for the eventuality of dependent predictor variables.
Bayesian networks overview
Bayesian network inference has multifaceted value in the interpretation of clinical data interpretation. The method was developed specifically to learn dependence structures from observational data (14,15). Generated graphs are intuitive and visually appealing, facilitating the comprehension of such outputs by non-statisticians. The structure of the inferred network may be used to infer causality, under some strong assumptions (16-18). Firstly, it is assumed that the observed data is representative of the true distribution. In a large random sample, this may be a reasonable assumption. Secondly, it is assumed that no unobserved factors influence the system. This is an inappropriate assumption in the medical field, as no hypothetical dataset of potential causative factors could ever be deemed exhaustive. It is assumed that each variable maintains independence of all other variables given, its direct causes and effects. This is analogous to the global Markov property (19). Finally, it is assumed that the true dependence structure of the studied variables may be represented by a directed acyclic graph. Some biological phenomena potentially violate this assumption. Feedback mechanisms, such as those found in metabolic and cardiovascular regulation are examples of graph cycles (20). Accordingly, we accept that the causal structure estimation we seek will provide a good approximation rather than a definitive result. Using cross-validation (21) and bootstrap approaches (22), a measure of confidence may be assigned to the reported network structure and parameters.
Bayesian network inference
A Bayesian network is a directed acyclic graphical representation of the joint probability distribution of a set of p random variables X (22). Therefore, a Bayesian network B may be denoted by the tuple G(V, Θ), in which G is a graph of V vertices and Θ parameters. A vertex Vi exists for each variable in X. Θ encodes the network parameters, such that:
Where pa(X:,i) are the parent vertices of X:,i in G (22). B encodes the probability distribution of X such that:
A graphical simplification of the Bayesian network is a representation as a graph G(V, E) of V vertices and V edges, such that an edge exists between Vi and Vj if and only if they are dependent. The task of Bayesian network learning is to isolate the most likely probability distribution which may have generated a matrix of values X. There are two primary subtasks associated with this problem, those of structure learning and parameter learning. Heuristic methods are employed to avoid the high computational complexity of exhaustive parameter search. Score-based models aim to maximise an objective based on a network score. We employ the Bayesian Information Criterion (BIC) and the Akaike Information Criterion (AIC) as network scoring methods.
In this paper, we apply Bayesian network inference to identify causative factors for several clinical phenomena associated with stroke. We examine data from the International Stroke Trial, detailing the clinical course of 19,000 episodes of stroke. We describe the feature-engineering, model assumptions and validation methods deployed to achieve and test our results.
Methods
Data preparation and cleaning
Data was mined from the repository of the International Stroke Trial 1 (IST-1) Database, hosted by the University of Edinburgh (23). IST-1 was a multicentre randomised trial of the efficacy of antithrombotic therapy in stroke. Patients were prescribed aspirin and/or unfractionated heparin according to a factorial design. The project was carried out at 437 centres in 36 countries. Detailed clinical documentation was performed during the trial, including specific features of the presentation, clinical examination, medication history and outcomes.
Feature exclusion
Recorded information was screened for clinical relevance. Variables relating to the specific time and hospital of presentation were excluded. Non-specific variables such as “other side effect of anticoagulation” were excluded. Free-text comments and dates of secondary diagnoses were excluded.
Feature modification
Categorical Features were extracted from the dataset. Two-class features such as “sex” were converted to binary variables. Features indicating clinical examination findings were assigned labels of class {“yes”, “no”, “cannot assess”}. These features were subsequently converted to binary features, such that positive labels were assigned in the case of “yes” or “cannot assess” and negative labels were assigned in the case of “no”. The etiological classification of the diagnosis was described by 4 mutually exclusive binary variables “ischaemic stroke”, “haemorrhagic stroke”, “unknown type”, “not stroke”. These features were encoded as a single categorical feature. 3-class categorical features were generated from numerical variables. Breakpoints between discrete factor levels were arbitrarily assigned to convenient intervals. Systolic blood pressure was converted to a 3-class categorical feature {“(0,140]”, “(140,220], “(220, 295]”}. A categorical feature was generated to describe mortality as follows:
A categorical variable was available indicating the Bamford Classification (24) of the stroke {“PACS”, “TACS”, “POCS”, “LACS”, “OTH”}. This was encoded as a five-class categorical feature without modification. Table 1 lists descriptions of all included variables.
Table 1
| Variable name | Description | Timepoint |
|---|---|---|
| Sex | M = male; F = female | Sex |
| Age | Age in years | Age |
| rasp3 | Aspirin within 3 days prior to randomisation | Recent_premorbid |
| rhep24 | Heparin within 24 hours prior to randomisation | Recent_premorbid |
| ratrial | Atrial fibrillation | Recent_premorbid |
| Aetiology | Aetiological classification of stroke | Aetiology |
| rsleep | Symptoms noted on waking | Symptom |
| rdelay | Delay between stroke and randomisation in hours | Prehospital |
| rvisinf | Infarct visible on CT | Presentation |
| rconsc | Conscious state at randomisation | Presentation |
| rsbp | Systolic blood pressure at randomisation | Presentation |
| rdef1 | Face deficit | Examination |
| rdef2 | Arm/hand deficit | Examination |
| rdef3 | Leg/foot deficit | Examination |
| rdef4 | Dysphasia | Examination |
| rdef5 | Hemianopia | Examination |
| rdef6 | Visuospatial disorder | Examination |
| rdef7 | Brainstem/cerebellar signs | Examination |
| bamford | Bamford classification of stroke | syndrome_diagnosis |
| rxasp | Trial aspirin allocated | randomisation |
| rxhep | Trial heparin allocated | randomisation |
| doac | Other anticoagulants | clinical_course |
| dgorm | Glycerol or manitol | clinical_course |
| dster | Steroids | clinical_course |
| dcaa | Calcium antagonists | clinical_course |
| dhaemd | Haemodilution | clinical_course |
| dcarend | Carotid surgery within 14 days | clinical_course |
| dmajnch | Major non-cerebral haemorrhage within 14 days | clinical_course |
| drsisc | Recurrent stroke of ischaemic aetiology within 14 days | clinical_course |
| drsh | Recurrent stroke of haemorrhagic aetiology within 14 days | clinical_course |
| drsunk | Recurrent stroke of unknown aetiology within 14 days | clinical_course |
| dpe | Pulmonary embolism within 14 days | clinical_course |
| dhep14 | Prescribed heparin for 14 days or until discharge or death | Day_14 |
| dasp14 | Aspirin given for 14 days or till death or discharge | Day_14 |
| dc14 | Discharged within 14 days | Day_14 |
| mortality_14 | Deceased within 14 days | Day_14 |
| outcome_6m | Condition at 6-month follow up | Follow_up_6 m |
Restriction
Thrombolysis was performed in 13 cases of the cohort (0.066%). All patients who underwent thrombolysis were excluded from analysis and this feature was removed from the dataset. All observations from the pilot study were excluded due to a change in the set of observed variables in the full study.
Missing values
One hundred and ninety-six observations (0.84%) contained at least one missing or unknown value. To determine whether the distribution of data absence was Missing at Random, 6-month mortality outcomes were modelled directly from data absence. This follows the approach of the dataset was converted according to the following function:
A generalised linear model was subsequently trained to predict death by 6-month follow up. The model failed to learn a significant association between missing data and death at 6 months (Accuracy =0.78, AccuracySD =0.00056, Kappa =0.0018, KappaSD =0.0028). Accordingly, missing values were assumed to be randomly distributed and all observations with missing values were excluded.
Temporal information
Temporal reasoning is a fundamental component of medical diagnosis and causal deduction (25), such that it is a criterion of the Bradford Hill criteria (26). Natural temporal relationships exist between many of the variables measured in the dataset. Each variable was assigned a clinical timepoint as appropriate. Using blacklisting (27), the model was prevented from learning arcs directed from latter timepoints to an earlier timepoints. Table 1 lists the timepoints of all included variables.
Graph inference
A discrete Bayesian network structure was chosen to represent the data. The model was generated using the R package “bnlearn” (27). Both the Hill-Climbing and Tabu algorithms were employed to perform score-based network inference. Each search algorithm was implemented using each of four network score functions – Bayesian Information Criterion, Akaike Information Criterion, Bayesian Dirichlet equivalent and K2. Each model was evaluated using 10 runs of 10-fold cross-validation. The optimal was selected as that achieving the highest cross validation likelihood.
Arc confidence was assessed using the non-parametric bootstrap technique described by Friedman et al. (22), in which a set of models is learned on bootstrap samples of the data. Equivalent networks are identified as graphs which contain the same set of conditional independence statements (22,28,29).
The non-parametric bootstrap procedure is carried out on a dataset D as follows (22,30):
Let G0(V, E0) be a Bayesian network representing the true dependence structure of X, composed of vertices V and edges E such that E ={e1,...ek}.
FOR b in {1,...m}:
- Db sampled using non-parametric bootstrap from X.
- A graphical model
is estimated from Db.
- END FOR
FOR EACH edge ei,j:
- Estimate the probability that each ei is present in the network structure by the frequency of its occurrence in the bootstrap sample graphs. Let 1{a} be the indicator function that condition α is true.
(II)
- END FOR EACH
Empirical probabilities of each edge,are known as arc strengths (30). They quantify confidence that ei,j is present in G0. Scutari presents a method to estimate the threshold of arc strength which optimally separates true edges from spurious ones (30). Let . Thereforeis an indicator of each edge’s presence in G0.
Let:
and
Therefore, t corresponds to the frequency of non-significant edges. Furthermore, t is the threshold above which an edge is present in Gtrue, such that:
Estimation of t is performed by minimisation of the following L1 normalised expression.
A set of 1,001 bootstrap network models were learned. A network average model was generated from this set, including arcs which were present in more than t of the generated models. This process was implemented with the “bnlearn” package (27).
Conditional independence testing
Mutual information, I, is a quantification of the co-dependence of two variables (31), such that:
Mutual Information may be considered as the reduction of the uncertainty in Xi achieved by observation of Xj. It is symmetrical, such that I (Xi, Xj) = I (Xj, Xi). Given a vertex Xi with a single parent Xj in a Bayesian network B, The mutual information between Xi and Xj describes Xi’s influence of on Xj and vice versa.
Let Ω(Xi) be the state space of Xi and ppr(Xi=a) be the prior probability of Xi to be in state a. The arc weight of is calculated as follows (31):
In the case that Xi has multiple parents {Xj, Xk:n} (31)
Inference testing was performed on the average-network graph using the asymptotic chi-squared test of mutual information.
Results
Model selection
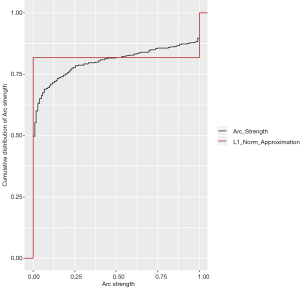
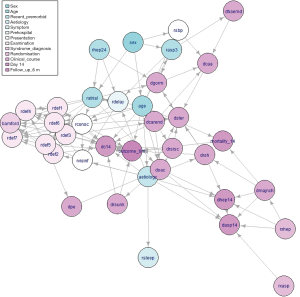
The tabu algorithm, using the k2 score demonstrated the optimal cross validation loglikelihood (tabu_k2: Mean = 1.52e+01, SD = 7.23e-04, CI.lower = 1.52e+01, CI.upper = 1.52e+01). Hill Climbing and Tabu search algorithms exhibited similar performance (Figure 1, Table 2). Scutari’s L1 normal approximation method (30) selected an arc strength significance cut-off of 0.5. Accordingly, 50.3% of all potential arcs were included in one or more network bootstraps (Figure 2). The final bayesian network estimate is illustrated in Figure 3.
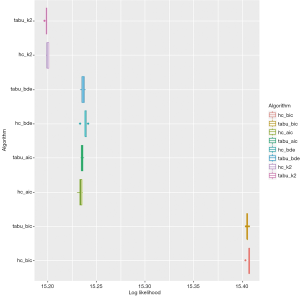
Table 2
| Score | Search algorithm | CV Log likelihood | SD | CI. lower | CI. upper |
|---|---|---|---|---|---|
| bic | hc | −15.406 | 0.002 | −15.403 | −15.407 |
| bic | tabu | −15.405 | 0.001 | −15.404 | −15.407 |
| aic | hc | −15.234 | 0.002 | −15.231 | −15.236 |
| aic | tabu | −15.235 | 0.001 | −15.234 | −15.237 |
| bde | hc | −15.238 | 0.003 | −15.234 | −15.242 |
| bde | tabu | −15.236 | 0.002 | −15.233 | −15.239 |
| k2 | hc | −15.2 | 0.001 | −15.198 | −15.201 |
| k2 | tabu | −15.198 | 0.001 | −15.197 | −15.199 |
A likelihood is estimated for the hypothesis that the validation set is generated from the estimated distribution. The natural logarithm of the likelihood is shown. The optimal method is selected to maximise the cross-validation log likelihood. 10 repeats of 10-fold cross-validation were performed. “bic”: Bayesian Information Criterion; “aic”: Akaike Information Criterion; “bde”: Bayesian Dirichlet equivalent; “k2” K2 score; “hc”: Hill Climbing algorithm; “tabu”: TABU search algorithm.
Demography
Sex was found to influence age at presentation (Mutual Info: P value <2e-16), prescription of aspirin in the 72 hrs prior to presentation (Mutual Info: P value <2e-16), atrial fibrillation on presentation (Mutual Info: P value <2e-16) and systolic blood pressure at randomisation (Mutual Info: P value <2e-16). Age at presentation influenced prescription of aspirin in the 72hrs prior to presentation (Mutual Info: P value <2e-16), atrial fibrillation on presentation (Mutual Info: P value <2e-16), stroke aetiology (Mutual Info: P value <2e-16), conscious level at presentation (Mutual Info: P value <2e-16), 14-day mortality (Mutual Info: P value <2e-16) and outcome at 6-month follow up (Mutual Info: P value <2e-16). Age at presentation was found to influence systolic blood pressure at randomisation (Mutual Info: P value <2e-16), visuospatial disorder risk (Mutual Info: P value <2e-16), prescription of other anticoagulants (Mutual Info: P value <2e-16) and discharge within 14 days (Mutual Info: P value <2e-16).
Recent history
Prescription of aspirin in the 72 hours prior to presentation influenced delay prior to randomisation (Mutual Info: P value <2e-16), prescription of glycerol or mannitol (Mutual Info: P value <2e-16) and haemodilution (Mutual Info: P value <2e-16). Prescription of heparin in the 24 hrs prior to presentation was found to influence atrial fibrillation on presentation (Mutual Info: P value =0.0022), delay prior to randomisation (Mutual Info: P value <2e-16) and prescription of glycerol or mannitol (Mutual Info: P value <2e-16). Atrial fibrillation on presentation influenced delay prior to randomisation (Mutual Info: P value <2e-16), conscious level at presentation (Mutual Info: P value <2e-16), dysphasia risk (Mutual Info: P value <2e-16) and hemianopia risk (Mutual Info: P value <2e-16). Atrial fibrillation on presentation affected visuospatial disorder risk (Mutual Info: P value <2e-16) and prescription of other anticoagulants (Mutual Info: P value <2e-16).
Event
Stroke aetiology was found to influence onset of symptoms on waking (Mutual Info: P value <2e-16), delay prior to randomisation (Mutual Info: P value <2e-16), infarct visibility (Mutual Info: P value <2e-16), upper limb deficit risk (Mutual Info: P value <2e-16), completion of aspirin prescription (Mutual Info: P value <2e-16) and discharge within 14 days (Mutual Info: P value <2e-16). Stroke aetiology affected prescription of corticosteroids (Mutual Info: P value <2e-16), haemorrhagic recurrence/transformation of stroke within 14 days (Mutual Info: P value <2e-16), recurrence of stroke of unknown aetiology within 14 days (Mutual Info: P value <2e-16) and cheparin prescription completion (Mutual Info: P value <2e-16).
Presentation
Delay prior to randomisation influenced infarct visibility (Mutual Info: P value <2e-16) and conscious level at presentation (Mutual Info: P value <2e-16). Infarct visibility was found to influence hemianopia risk (Mutual Info: P value <2e-16) and visuospatial disorder risk (Mutual Info: P value <2e-16). Conscious level at presentation was found to influence infarct visibility (Mutual Info: P value <2e-16), facial deficit risk (Mutual Info: P value <2e-16), upper limb deficit risk (Mutual Info: P value <2e-16) and lower limb deficit risk (Mutual Info: P value <2e-16). Conscious level at presentation influenced dysphasia risk (Mutual Info: P value <2e-16), hemianopia risk (Mutual Info: P value <2e-16), visuospatial disorder risk (Mutual Info: P value <2e-16) and brainstem and cerebellar deficit risk (Mutual Info: P value <2e-16). Conscious level at presentation affected Bamford classification (Mutual Info: P value <2e-16), prescription of corticosteroids (Mutual Info: P value <2e-16), discharge within 14 days (Mutual Info: P value <2e-16) and outcome at 6-month follow up (Mutual Info: P value <2e-16). Systolic blood pressure at randomisation influenced prescription of calcium channel blockers (Mutual Info: P value <2e-16). Presence of a facial deficit on examination exerted influence on Bamford classification (Mutual Info: P value <2e-16), prescription of glycerol or mannitol (Mutual Info: P value <2e-16) and discharge within 14 days (Mutual Info: P value <2e-16).
Clinical examination
Presence of an upper limb deficit on examination exerted influence on facial deficit risk (Mutual Info: P value <2e-16), lower limb deficit risk (Mutual Info: P value <2e-16), dysphasia risk (Mutual Info: P value <2e-16) and brainstem and cerebellar deficit risk (Mutual Info: P value <2e-16). Presence of an upper limb deficit on examination influenced Bamford classification (Mutual Info: P value <2e-16) and discharge within 14 days (Mutual Info: P value =0.0496). Presence of a lower limb deficit on examination influenced facial deficit risk (Mutual Info: P value <2e-16), dysphasia risk (Mutual Info: P value <2e-16), brainstem and cerebellar deficit risk (Mutual Info: P value <2e-16) and Bamford classification (Mutual Info: P value <2e-16). Presence of a lower limb deficit on examination influenced likelihood of carotid endarterectomy within 14 days (Mutual Info: P value <2e-16), discharge within 14 days (Mutual Info: P value <2e-16) and outcome at 6-month follow up (Mutual Info: P value <2e-16). Dysphasia affected facial deficit risk (Mutual Info: P value <2e-16), brainstem and cerebellar deficit risk (Mutual Info: P value <2e-16) and Bamford classification (Mutual Info: P value <2e-16). Hemianopia exerted influence on facial deficit risk (Mutual Info: P value <2e-16), lower limb deficit risk (Mutual Info: P value <2e-16), dysphasia risk (Mutual Info: P value <2e-16) and brainstem and cerebellar deficit risk (Mutual Info: P value <2e-16). Hemianopia influenced Bamford classification (Mutual Info: P value <2e-16), pulmonary embolism within 14 days (Mutual Info: P value <2e-16) and outcome at 6-month follow up (Mutual Info: P value <2e-16). Presence of visuospatial disorders on examination exerted influence on upper limb deficit risk (Mutual Info: P value <2e-16), lower limb deficit risk (Mutual Info: P value <2e-16), dysphasia risk (Mutual Info: P value <2e-16) and hemianopia risk (Mutual Info: P value <2e-16). Presence of visuospatial disorders on examination was found to influence brainstem and cerebellar deficit risk (Mutual Info: P value <2e-16), Bamford classification (Mutual Info: P value <2e-16) and discharge within 14 days (Mutual Info: P value <2e-16). Presence of brainstem/cerebellar deficits on examination influenced facial deficit risk (Mutual Info: P value <2e-16) and Bamford classification (Mutual Info: P value <2e-16). Allocation to the aspirin trial arm influenced completion of aspirin prescription (Mutual Info: P value <2e-16).
Management
Allocation to the heparin trial arm affected risk of major non-cerebral haemorrhage within 14 days (Mutual Info: P value <2e-16), completion of heparin prescription (Mutual Info: P value <2e-16) and completion of aspirin prescription (Mutual Info: P value <2e-16). Prescription of other anticoagulants affected recurrence risk for ischaemic stroke within 14 days (Mutual Info: P value <2e-16), completion of heparin prescription (Mutual Info: P value <2e-16) and completion of aspirin prescription (Mutual Info: P value <2e-16). Prescription of glycerol or mannitol was found to influence prescription of corticosteroids (Mutual Info: P value <2e-16) and prescription of calcium channel blockers (Mutual Info: P value <2e-16). Prescription of calcium channel blockers was found to influence prescription of corticosteroids (Mutual Info: P value <2e-16). Haemodilution influenced prescription of calcium channel blockers (Mutual Info: P value <2e-16). Carotid endarterectomy within 14 days influenced prescription of other anticoagulants (Mutual Info: P value =0.0024), prescription of corticosteroids (Mutual Info: P value =0.0002) and recurrence of ischaemic stroke within 14 days (Mutual Info: P value <2e-16).
Clinical course
Major non-cerebral haemorrhage within 14 days affected likelihood of haemorrhagic recurrence/transformation of stroke within 14 days (Mutual Info: P value =0.0002), completion of heparin prescription (Mutual Info: P value <2e-16), completion of aspirin prescription (Mutual Info: P value <2e-16) and 14-day mortality (Mutual Info: P value <2e-16). Recurrence of ischaemic stroke within 14 days influenced prescription of corticosteroids (Mutual Info: P value <2e-16), discharge within 14 days (Mutual Info: P value <2e-16) and outcome at 6-month follow up (Mutual Info: P value <2e-16). Haemorrhagic recurrence/transformation of stroke within 14 days affected prescription of glycerol or mannitol (Mutual Info: P value =0.0066), prescription of corticosteroids (Mutual Info: P value =0.0002), completion of heparin prescription (Mutual Info: P value <2e-16) and outcome at 6-month follow up (Mutual Info: P value <2e-16). Recurrence of stroke of unknown aetiology within 14 days was found to influence discharge within 14 days (Mutual Info: P value <2e-16) and outcome at 6-month follow up (Mutual Info: P value <2e-16). Pulmonary Embolism within 14 days was found to influence prescription of other anticoagulants (Mutual Info: P value <2e-16). Completion of heparin prescription affected completion of aspirin prescription (Mutual Info: P value <2e-16). Discharge within 14 days affected outcome at 6-month follow up (Mutual Info: P value <2e-16). Fourteen-day mortality affected outcome at 6-month follow up (Mutual Info: P value <2e-16).
Specific outcomes: morbidity and mortality
Fourteen-day mortality risk was highest in the (75,99] age bracket (RR =2.8806, ARI =0.0296, P value ≤2.22e-16), and lowest in under 55s (RR =0.272, ARI =-2.20e-02, P value =7.78e-143). Major non-cerebral haemorrhage also increased mortality risk (RR =6.44e+00, ARI =1.47e-01, P value <2.22e-16). Higher age at presentation adversely affected 6-month outcomes (Mutual information P value: <2.22e-16) independently of its effect on short term mortality. This effect included an increased risk of death prior to 6-month follow up in the 55–75 years group (RR =7.39e-01, ARI =-1.53e-01, P value <2.22e-16) and the 75–99 years group (RR =1.999, ARI =0.256, P value <2.22e-16). Conscious level at presentation also adversely affected 6-month mortality independent of 14-day mortality (Mutual information P value: <2.22e-16). Patients who were unconscious at presentation accepted an increased risk of dependence (RR =23.576, ARI =0.0201, P value <2.22e-16) and death (RR =11.809, ARI =0.0434, P value <2.22e-16) at follow up. Stroke recurrence was associated with poorer outcomes regardless of whether the aetiology was ischaemic (Mutual information P value <2.22e-16), haemorrhagic (Mutual information P value <2.22e-16) or unknown (Mutual information P value: <2.22e-16). Patients who were fit to be discharged within 14 days of presentation experienced favourable 6-month outcomes (Mutual information P value <2.22e-16), including a decreased risk of dependency (RR =0.387, ARI =-0.348, P value <2.22e-16) and death (RR =2.72e-01, ARI =−3.02e-01, P value <2.22e-16).
Specific outcomes: recurrence
Stroke recurrence risk varied with aetiology. Presentation with haemorrhagic stroke greatly increased risk of recurrence haemorrhage (RR =8.05e+00, ARI =2.11e-01, P value <2.22e-16). Although presentation with ischaemic stroke increased risk of recurrence of stroke of unknown aetiology (RR =4.02e+00, ARI =1.19e-01, P value <2.22e-16) it was not found to independently influence ischaemic stroke recurrence. Patients who suffered major non cerebral haemorrhage undertook an increased risk of haemorrhagic stroke recurrence (RR =9.05, ARI =0.06, P value =1.54e-05).
Discussion
Consistent arcs
The structure inference algorithm successfully learned a network which is largely consistent with clinical knowledge. Vertices representing clinical examination findings were densely interconnected, and clusters within this region reflected clinical syndromes.
For instance, the presence of brainstem or cerebellar deficits on clinical examination was found to depend on the presence of visuospatial disorders. Visuospatial disorders indicate occipital lobe pathology and therefore posterior circulation deficiency. The cerebellum is also supplied by the posterior circulatory system. Applying causal reasoning to this interaction, visuospatial disorders and cerebellar deficits share a common causative factor—posterior circulatory disruption. As this factor is unobserved, confounding occurs between the two child nodes. Consequently, an apparent causal relationship is observed from visuospatial disorders to cerebellar disorders. Nonetheless, detection of the association between these clinical features appropriately identifies their special relationship.
Each neurological deficit exerted some influence on the Bamford Classification. Bamford Classification is an objective clinical sign which is assigned by a clinician based on the cluster of neurological deficits found on exam. Thus, these dependencies are consistent with the true clinical process. Visibility of the infarct depended on delay prior to randomisation aetiology of the stroke, this is consistent with the increasing visibility of infarcts over time. Stroke aetiology also influenced the visibility of the stroke, this is likely due to the exclusion of all patients with visible intracranial haemorrhage at the time of recruitment.
Prescription of calcium antagonists was influenced by systolic blood pressure and concomitant prescription of glycerol or mannitol. As these features represent the indication and alternatives to calcium antagonist medications respectively, this association is clinically consistent. Prescription of other anticoagulants depended on occurrence of pulmonary embolism.
Age at presentation depended on sex of the patient. This is a likely consequence of the known difference between the age profile of strokes in males and females, with males suffering earlier events (32). Delay prior to randomisation was lower in patients who received heparin within the previous 24 hours. As this relationship is independent of stroke aetiology, it may indicate earlier detection of stroke in patients previously interacting with health services.
Inconsistent arcs and latent features
Infarct visibility depended directly on conscious level at presentation. Although it is conceivable that these events are associated, it is probable that some other latent feature such as infarct size influenced both of these variables. Carotid endarterectomy was directly linked to the presence of a lower limb deficit. Carotid endarterectomy is indicated due to carotid stenosis, a cause of ischaemic stroke—therefore, it is likely that aetiology d-separates carotid endarterectomy and lower limb deficits in the true causality network.
Model selection and regularisation
Bayesian network inference detected 119 conditional dependencies in the International Stroke Trial dataset. In the majority cases, these associations were consistent with known clinical phenomena. Few associations were detected which were not clinically explicable. It is notable that the selection of the arc strength significance cut-off critically affected the resultant network structure, as several arcs had strengths near the threshold. Approximately half of all potential arcs were deemed significant in more than one bootstrap network estimate, indicating moderate variability of the network estimate.
Conclusions
We organise the pathogenesis, management and sequelae as a single functional system, in which clinical events are assumed to influence one another naturally. We have demonstrated the utility of the method to form and test multiple hypotheses in a highly objective fashion.
This feature efficiently addresses the dual problems of hypothesis search and multiple hypothesis testing. Though true evidence of causality may only be attained through interventional research (17,18), complete observation of the causative process allow its improved approximation. In this analysis, we demonstrate the interdependent nature of many factors which are known to be associated with stroke risk. This methodology is general and may theoretically be applied to various observational datasets across the health sciences.
Acknowledgments
The author would like to thank Professor Peter Sandercock and the IST1 collaboration for provision of the International Stroke Trial data. The author would like to thank Reecha Sofat and Dionisio Acosta Mena for their guidance.
This research was funded by National Institute for Health Research Biomedical Research Centre and a University College London Hospital Levi Fellowship. The project was supported by the National Institute for Health Research University College London Hospitals Biomedical Research Centre. The funders of this analysis had no role in the study design; gathering, analysis and interpretation of these data; writing of the report; and decision to submit the report for publication. The corresponding author had full access to all data; takes responsibility for the integrity of these data and the accuracy of the analysis; and takes final responsibility for the decision to submit for publication.
Funding: None.
Footnote
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/jmai.2019.09.01). RO serves as an unpaid editorial board member of Journal of Medical Artificial Intelligence from May 2020 to Apr 2022.
Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All patient data used in this analysis is fully anonymised and available via the University of Edinburgh Data Share repository. This analysis is performed on data which was originally collected and analysed during the International Stroke Trial by the IST1 collaboration. This data was accessed and reanalysed with the permission and review of Peter Sandercock, principal investigator of the International Stroke Trial.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- World Health Organization. Global Health Estimates 2016: Disease Burden by Cause, Age, Sex, by Country and by Region, 2000-2016. Geneva, 2018.
- Al-Harazi O, Al Insaif S, Al-Ajlan MA, et al. Integrated Genomic and Network-Based Analyses of Complex Diseases and Human Disease Network. J Genet Genomics 2016;43:349-67. [Crossref] [PubMed]
- Schimit PHT, Pereira FH. Disease spreading in complex networks: A numerical study with Principal Component Analysis. Expert Syst Appl 2018;97:41-50. [Crossref]
- Caldera M, Buphamalai P, Müller F, et al. Interactome-based approaches to human disease. Curr Opin Syst Biol 2017;3:88-94. [Crossref]
- Goh KI, Cusick ME, Valle D, et al. The human disease network. Proc Natl Acad Sci U S A 2007;104:8685-90. [Crossref] [PubMed]
- Wang Y, Zeng J. Predicting drug-target interactions using restricted Boltzmann machines. Bioinformatics 2013;29:i126-34. [Crossref] [PubMed]
- Wang RS, Loscalzo J. Network-Based Disease Module Discovery by a Novel Seed Connector Algorithm with Pathobiological Implications. J Mol Biol 2018;430:2939-50. [Crossref] [PubMed]
- Wu Z, Li W, Liu G, et al. Network-Based Methods for Prediction of Drug-Target Interactions. Front Pharmacol 2018;9:1134. [Crossref] [PubMed]
- King G, Zeng L. Logistic Regression in Rare Events Data. Polit Anal 2001;9:137-63. [Crossref]
- Korb KB, Nicholson AE. Bayesian Artificial Intelligence, Second Edition. 2nd ed. Boca Raton, FL, USA: CRC Press, Inc., 2010.
- Strobl R, Stucki G, Grill E, et al. Graphical models illustrated complex associations between variables describing human functioning. J Clin Epidemiol 2009;62:922-33. [Crossref] [PubMed]
- Röhrig N, Strobl R, Müller M, et al. Directed acyclic graphs helped to identify confounding in the association of disability and electrocardiographic findings: results from the KORA-Age study. J Clin Epidemiol 2014;67:199-206. [Crossref] [PubMed]
- Liddicoat C, Bi P, Waycott M, et al. Landscape biodiversity correlates with respiratory health in Australia. J Environ Manage 2018;206:113-22. [Crossref] [PubMed]
- Korb KB, Nicholson AE. Bayesian Artificial Intelligence. Technometrics 2005;47:101-2. [Crossref]
- Zhang X, Yuan Z, Ji J, et al. Network or regression-based methods for disease discrimination: a comparison study. BMC Med Res Methodol 2016;16:100. [Crossref] [PubMed]
- Pearl J. The causal foundations of structural equation modeling. In: Hoyle RH. editor. Handbook of Structural Equation Modeling. New York: The Guilford Press, 2012:68-91.
- Pearl J. An Introduction to Causal Inference. Int J Biostat 2010;6:7. [Crossref] [PubMed]
- Pearl J. Causality: Models, Reasoning and Inference. Cambridge University Press, 2009.
- Lauritzen SL. Graphical Models. Oxford University Press, 1996.
- Legramante JM, Raimondi G, Massaro M, et al. Positive and Negative Feedback Mechanisms in the Neural Regulation of Cardiovascular Function in Healthy and Spinal Cord-Injured Humans. Circulation 2001;103:1250-5. [Crossref] [PubMed]
- Russell S, Norvig P. Artificial Intelligence A Modern Approach Third Edition. Pearson 2010:1151.
- Friedman N, Goldszmidt M, Wyner A. Data Analysis with Bayesian Networks: A Bootstrap Approach 2013.
- The International Stroke Trial (IST): a randomised trial of aspirin, subcutaneous heparin, both, or neither among 19435 patients with acute ischaemic stroke. International Stroke Trial Collaborative Group. Lancet 1997;349:1569-81. [Crossref] [PubMed]
- Bamford J, Sandercock P, Dennis M, et al. Classification and Natural History of Clinically Identifiable Subtypes of Cerebral Infarction. Lancet 1991;337:1521-6. [Crossref] [PubMed]
- Long W. Temporal reasoning for diagnosis in a causal probabilistic knowledge base. Artif Intell Med 1996;8:193-215. [Crossref] [PubMed]
- Wasserman EA, Kao SF, Van Hamme LJ, et al. Causation and Association. In: Psychology of Learning and Motivation - Advances in Research and Theory, 1996:207-64.
- Scutari M. Learning Bayesian Networks with bnlearn R package 2010;35(3).
- Meek C. Causal inference and causal explanation with background knowledge. In: Proceedings of 11th Conference on Uncertainty in Artificial Intelligence. 1995:403-18.
- Chickering DM. A Transformational Characterization of Equivalent Bayesian Network Structures 2013.
- Scutari M, Nagarajan R. On Identifying Significant Edges in Graphical Models. In: Proceedings of the Workshop ’Probabilistic Problem Solving in Biomedicine’ of the 13th Artificial Intelligence in Medicine (AIME) Conference 2011:15-27.
- Nicholson AE, Jitnah N. Using mutual information to determine relevance in Bayesian networks. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 1998:399-410.
- Petrea RE, Beiser AS, Seshadri S, et al. Gender differences in stroke incidence and poststroke disability in the Framingham heart study. Stroke 2009;40:1032-7. [Crossref] [PubMed]
Cite this article as: O’Shea R. Understanding stroke with Bayesian networks. J Med Artif Intell 2020;3:2.


